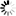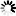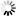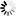隨著電子商務(wù)產(chǎn)業(yè)的飛速發(fā)展，物流行業(yè)業(yè)務(wù)量持續(xù)增長。物流行業(yè)業(yè)務(wù)量的增長對物流企業(yè)的調(diào)度能力提出了更高的要求。同時(shí)，像智能物流機(jī)器人、自動化分揀包裝設(shè)備、無人駕駛車輛以及無人機(jī)等以新一代信息技術(shù)為支撐、運(yùn)作管理更為高效、貨物運(yùn)輸更為便捷的智慧物流在我國快速發(fā)展，為物流業(yè)轉(zhuǎn)型升級提供了更多可能。在此背景下，一種車輛與無人機(jī)協(xié)同進(jìn)行配送的模式受到了物流行業(yè)和學(xué)術(shù)界的廣泛關(guān)注，車輛與無人機(jī)組合模式如圖1所示。車輛與無人機(jī)協(xié)同進(jìn)行配送的模式有效地結(jié)合了無人機(jī)速度快、通行能力強(qiáng)的優(yōu)勢以及傳統(tǒng)運(yùn)輸車輛優(yōu)秀的載重、續(xù)航能力，為物流配送降本增效提供了新的解決方案。本文將從數(shù)學(xué)模型以及求解算法兩個方面對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題進(jìn)行綜述。

 

圖1 車輛與無人機(jī)組合模式示意圖   

 

1 車輛與無人機(jī)協(xié)同配送路徑規(guī)劃模型

圖2 車輛與無人機(jī)協(xié)同配送模式示意圖   

 

車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題主要分為單車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題(Traveling Saleman Problem with Drones, TSPD)和多車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題(Vehicle Routing Problem with Drones, VRPD)。Murray和Chu[1]首先對車輛與無人機(jī)協(xié)同配送車輛路徑規(guī)劃問題展開研究，提出了無人機(jī)協(xié)同配送的旅行商問題(the Flying Sidekick Traveling Saleman Problem, FSTSP),并建立了以最小化總配送時(shí)間為目標(biāo)的混合整數(shù)規(guī)劃模型(Mix Integer Progroming, MIP)。在其研究中車輛與無人機(jī)協(xié)同進(jìn)行物流配送，車輛在運(yùn)輸包裹的同時(shí)，作為一個承擔(dān)無人機(jī)發(fā)射、回收以及更換電池任務(wù)的移動平臺。此外，配送任務(wù)由一輛僅配備一架無人機(jī)的車輛承擔(dān)，且無人機(jī)單次發(fā)射僅能服務(wù)一個客戶，無人機(jī)可以在某個客戶點(diǎn)處從車輛進(jìn)行發(fā)射，并在完成計(jì)劃的配送任務(wù)之后，在另外一個與發(fā)射點(diǎn)不同的客戶點(diǎn)處與車輛進(jìn)行匯合。車輛與無人機(jī)協(xié)同配送模式如圖2所示。該模型的提出受到了國內(nèi)外學(xué)者的廣泛關(guān)注，隨后的相關(guān)研究基于不同的應(yīng)用場景分別從優(yōu)化目標(biāo)、約束等角度對于車輛與無人機(jī)協(xié)同配送路徑規(guī)劃模型進(jìn)行了拓展。

 

1.1 優(yōu)化目標(biāo)

在關(guān)于車輛與無人機(jī)協(xié)同配送路徑規(guī)劃模型的相關(guān)研究中，從優(yōu)化目標(biāo)來看，最常見的優(yōu)化目標(biāo)主要包括配送時(shí)間、配送成本以及碳排放量等。

 

針對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題，Murray和Chu [1]建立了以最小化總配送時(shí)間為目標(biāo)的混合整數(shù)規(guī)劃模型，即使車輛和無人機(jī)完成對所有客戶的配送服務(wù)后回到配送中心的時(shí)間最短。Wang等[2]同樣以最小化總配送時(shí)間為目標(biāo)對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題進(jìn)行了研究，其研究結(jié)果表明，與僅使用車輛進(jìn)行配送相比，無人機(jī)的使用可以節(jié)省大量時(shí)間。Luo等 [3]同樣以最小化總配送時(shí)間為目標(biāo)對車輛與無人機(jī)協(xié)同配送的路徑規(guī)劃問題展開了研究，其研究中考慮了車輛可以搭載多架無人機(jī)且無人機(jī)單次發(fā)射可以服務(wù)多個客戶的情況，與無人機(jī)每次發(fā)射僅能服務(wù)單個客戶相比，允許無人機(jī)每次發(fā)射可對多個客戶進(jìn)行服務(wù)可有效減少配送時(shí)間。

 

Sacramento等[4]基于Murray和Chu提出的FSTSP模型建立了在滿足容量和時(shí)間約束的前提下以最小化總成本為目標(biāo)的混合整數(shù)規(guī)劃模型。其中，總成本包括車輛和無人機(jī)的配送成本。此外，在考慮車輛和無人機(jī)的配送成本的基礎(chǔ)上，高嬌嬌和郭秀萍[5]進(jìn)一步將車輛、無人機(jī)的固定成本納入考慮。而Ha等[6]則將無人機(jī)和車輛在客戶點(diǎn)處相互等待的時(shí)間作為懲罰成本納入到總成本當(dāng)中。

 

此外，Chiang等[6]和Kuo等[8]還以減少碳排放為優(yōu)化目標(biāo)對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題展開了研究，證明了無人機(jī)參與配送對于減少碳排放的積極作用。據(jù)統(tǒng)計(jì)，交通運(yùn)輸業(yè)產(chǎn)生的碳排放占全球碳排放總量的14%,而公路運(yùn)輸則占據(jù)了交通運(yùn)輸業(yè)碳排放的四分之三[9,10]。因此，減少物流配送過程中產(chǎn)生的碳排放具有重要意義。

 

1.2 約束條件

約束條件的設(shè)置是對問題背景環(huán)境的復(fù)現(xiàn)，是模型中不可或缺的部分。由于應(yīng)用場景的不同或是出于簡化模型的目的，各項(xiàng)研究中約束條件也不盡相同。

 

在車輛與無人機(jī)協(xié)同配送的路徑規(guī)劃問題中，所使用的車輛與無人機(jī)的數(shù)量對相關(guān)約束的構(gòu)建有著重要影響，是研究人員們關(guān)注的重點(diǎn)。在Murray和Chu[1]的研究中，僅由一輛搭載一架無人機(jī)的車輛承擔(dān)配送任務(wù)，且無人機(jī)每次發(fā)射只能對一個客戶進(jìn)行服務(wù)。隨后的相關(guān)研究從多個角度進(jìn)行了拓展，如增加車輛可搭載的無人機(jī)數(shù)量[11,12]或是假設(shè)無人機(jī)每次發(fā)射可以對多個客戶進(jìn)行服務(wù)[3,13]等。而Wang等[2]進(jìn)一步將FSTSP問題拓展為多車輛與無人機(jī)協(xié)同進(jìn)行配送的車輛路徑規(guī)劃問題，該項(xiàng)研究中由一隊(duì)搭載無人機(jī)的車輛承擔(dān)配送任務(wù)。

 

在車輛與無人機(jī)協(xié)同配送的路徑規(guī)劃問題中，如何構(gòu)建無人機(jī)的續(xù)航模型也是車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題中備受關(guān)注的一點(diǎn)。在現(xiàn)有研究中通常使用最大飛行距離、最長續(xù)航時(shí)間以及依賴于包裹重量的線性能量消耗模型[14]對無人機(jī)的續(xù)航進(jìn)行表征，而這些過于簡化的續(xù)航模型可能會對無人機(jī)的續(xù)航能力帶來錯誤的估計(jì)。Murray等[11]在其研究中引入了Liu 等[15]推導(dǎo)的以無人機(jī)包裹重量以及無人機(jī)飛行速度為自變量的非線性能量消耗模型對無人機(jī)的續(xù)航能力進(jìn)行表征。其對比了上述四種不同的無人機(jī)續(xù)航模型，發(fā)現(xiàn)相較于非線性能量消耗模型，應(yīng)用其它幾種續(xù)航模型有較大的風(fēng)險(xiǎn)導(dǎo)致求解結(jié)果為不可行解。

 

此外，在實(shí)際的物流配送場景中，客戶可以接受服務(wù)的時(shí)間通常位于一個時(shí)間區(qū)間內(nèi)，該時(shí)間區(qū)間可以用時(shí)間窗約束進(jìn)行表示[16]。目前，針對考慮時(shí)間窗約束的車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題的研究較少。針對該問題，Kuo等[17]建立了一個混合整數(shù)規(guī)劃模型，其研究中假設(shè)車輛、無人機(jī)對客戶進(jìn)行服務(wù)的時(shí)間需要位于客戶點(diǎn)的時(shí)間窗內(nèi)。其研究結(jié)果表明，對于時(shí)間窗的考慮會使得配送成本進(jìn)一步增加，但相比于僅使用車輛的配送模式，無人機(jī)的使用可以有效降低配送成本。

 

2 求解算法

2.1 精確算法

部分文獻(xiàn)采用精確算法對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題進(jìn)行求解，包括采用Gurobi、CPLEX等商業(yè)求解器對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃模型直接進(jìn)行求解、設(shè)計(jì)分支定界算法(branch-and-bound algorithm, B&B)以及設(shè)計(jì)動態(tài)規(guī)劃(Dynamic Programming, DP)方法等。車輛與無人機(jī)協(xié)同配送的路徑規(guī)劃問題屬于NP-hard問題，精確算法在小規(guī)模算例的求解上表現(xiàn)出色，可以確保找到最優(yōu)的解決方案，但在大規(guī)模問題上的計(jì)算復(fù)雜度較高，需要大量的計(jì)算資源。在針對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題的相關(guān)研究中，常使用商業(yè)求解器對所構(gòu)建數(shù)學(xué)模型在小規(guī)模算例上進(jìn)行求解，并將求解結(jié)果作為對照以驗(yàn)證所設(shè)計(jì)算法的精確性和高效性。而Wang等[18]開發(fā)了能夠找到高質(zhì)量解的分支定價(jià)算法(Branch-and-Price algorithm, B&P)來求解車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題。而Bouman等[19]和Tang等[20]則分別采用動態(tài)規(guī)劃和約束規(guī)劃(Constraint Programming, CP)方法來求解車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題。

 

2.2 啟發(fā)式算法

對于大規(guī)模問題，若采用精確算法求解，即使花費(fèi)大量時(shí)間也很難找到可行的解決方案。與精確算法相比，啟發(fā)式算法可以在較短的時(shí)間內(nèi)為大規(guī)模問題找到的近似最優(yōu)的解決方案。Ha等[6]設(shè)計(jì)了一種貪婪隨機(jī)自適應(yīng)搜索算法(Greedy Randomized Adaptive Search Procedure, GRASP)用于解決優(yōu)化目標(biāo)為最小化總配送時(shí)間或最小化總配送成本的車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題，該算法可有效求解客戶數(shù)量多達(dá)100個的大模型算例。Poikonen等[21]設(shè)計(jì)了四種基于分支定界算法的啟發(fā)式算法用于求解車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題，針對包含200個節(jié)點(diǎn)的大規(guī)模算例，該算法的平均求解時(shí)間不超過15秒。而Sacramento等[4]提出了一種自適應(yīng)大鄰域搜索算法(Adaptive Large Neighborhood Search, ALNS)用于求解車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題，該算法通過采用多種針對問題特性設(shè)計(jì)的破壞算子和修復(fù)算子對當(dāng)前解進(jìn)行重構(gòu)以改進(jìn)當(dāng)前解。針對考慮時(shí)間窗的車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題，Kuo等[17]提出一種變鄰域搜索算法(Variable Neighborhood Search, VNS)對該問題進(jìn)行求解。研究結(jié)果表明，相對于Sacramento設(shè)計(jì)的自適應(yīng)大鄰域搜索算法，變鄰域搜索算法具有更好的性能，且兩者間的差距隨著算例規(guī)模的增大而增大。

 

3 總結(jié)

本文綜合車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題的相關(guān)研究，回顧了車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題的常見優(yōu)化目標(biāo)，包括配送時(shí)間、配送成本和碳排放量等，探究了車輛與無人機(jī)協(xié)同配送路徑規(guī)劃模型的約束中考慮的影響因素，如車輛與無人機(jī)的數(shù)量、無人機(jī)續(xù)航模型以及時(shí)間窗。此外，基于已有文獻(xiàn)回顧了用于求解車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題的常見算法，包括精確算法和啟發(fā)式算法。

 

綜合來看，車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題的研究為提升物流企業(yè)的調(diào)度能力，使其能高效地進(jìn)行路徑規(guī)劃提供了重要的理論支持。在今后研究中應(yīng)關(guān)注如何設(shè)計(jì)適用更廣泛場景的數(shù)學(xué)模型以及更靈活高效的算法。此外，機(jī)器學(xué)習(xí)算法已經(jīng)成功應(yīng)用于車輛的路徑規(guī)劃問題當(dāng)中，而現(xiàn)有針對車輛與無人機(jī)協(xié)同配送路徑規(guī)劃算法的研究中大多都是采用精確算法或者啟發(fā)式算法進(jìn)行求解，機(jī)器學(xué)習(xí)算法在車輛與無人機(jī)協(xié)同配送路徑規(guī)劃問題中的應(yīng)用有待進(jìn)一步加強(qiáng)。